:: Theoretical Background
Tensor goes back to the Weaire–Phelan structure, which is a complex 3-dimensional structure representing an idealised foam of equal-sized bubbles. In 1993 Denis Weaire and Robert Phelan, two physicists based at Trinity College Dublin, found that in computer simulations of foam, this structure was a better solution of the “Kelvin problem” than the previous best-known solution, the Kelvin structure.
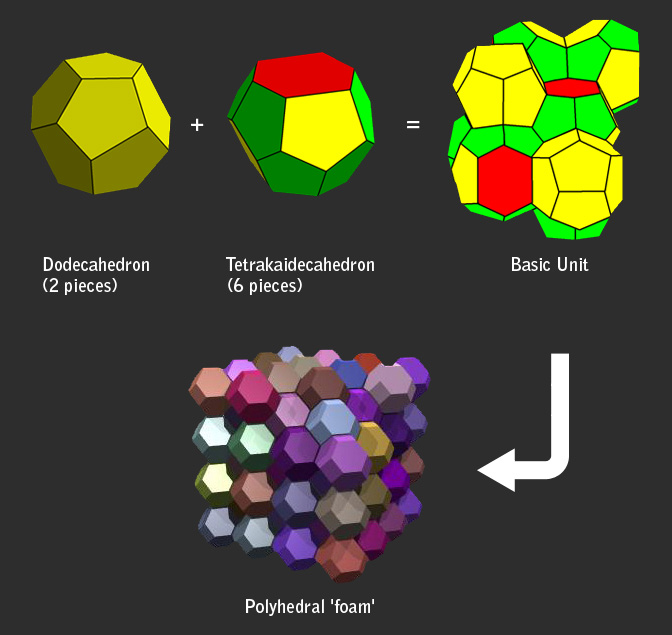
The Weaire–Phelan structure differs from Kelvin’s in that it uses two kinds of cells, though they both have equal volume.
One is an irregular dodecahedron with pentagonal faces, possessing tetrahedral symmetry (Th).
Tetrakaidecahedron
The second is a tetrakaidecahedron with two hexagonal and twelve pentagonal faces possessing antiprismatic symmetry (D2v). (This figure is also called a tetradecahedron; this article uses Weaire and Phelan’s name.)
Like the hexagons in the Kelvin structure, the pentagons in both types of cells are slight ly curved. The surface area of the Weaire–Phelan structure is 0.3% less than that of the Kelvin structure. It has not been proved that the Weaire–Phelan structure is optimal, but as of 2009 no better structure has been found.
:: Construction
By unwrapping a 3 dimeonsional object, you can get a 2 dimensional cut-pattern. We use a kind of polyethylene material and bring the plastic boards by laser-cut technology in shape. Franz Piffl’s turn starts here.
After that you get a well cut pattern with buckling edges. 2 boards were needed to get one object.
Several tests concerning the connection within one object and between two objects were needed before we decided to use special adhesive tape.
After uncounted amount of working hours our first Tensor armada was finished!
:: Tensor 48 11’33.67″ N / 16 20’44.00″ E
The first configuration of the Tensor was made for the Sound:Frame festival 2010. The coordinates in the name of the artwork defines the place/location, where it is standing. In our case defines that a certain configuration/structure of the objects.
